表面積(ひょうめんせき)は、立体図形の表面の面積。 直感的には、立体図形を水中に入れたとき濡れる部分の面積のことである。 ユークリッド空間で、図形を a 倍に拡大すると、体積は a 3 倍になるのに対し、表面積は a 2 倍になる。 ただし、3軸それぞれの方向に a 球の表面積・・・4πr² r³を微分すると3r²になります。 つまり、球の体積を微分すると円の表面積の公式になります。 そもそも微分とは、『少しの増加の間の変化量』を表現しています。 円の面積のちょこっとの増加分は円の周りの長さに相当します。球の表面積、体積の解答 表面積は 4 π ⋅ 4 2 = 64 π cm 2 体積は 4 3 π ⋅ 4 3 = 256 3 π cm 3 1辺 8 cm の立方体の表面積は、 6 × 8 2 = 384 cm 2 直径 10 cm の球の半径は 5 cm なので、表面積は 4 π ⋅ 5 2 = 100 π ≒ 100 × 314 = 314 cm 2 よって、1辺 8 cm の立方体の表面積の方
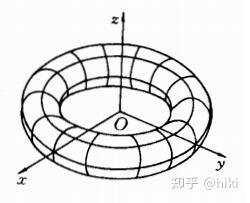
圆环体的体积和表面积怎么算 知乎
表面積 体積 問題
表面積 体積 問題- n次元球の定義 n 次元球というのは n 次元の球です。 ちゃんと言うと、 n 次元空間内の「ある点」からの (ユークリッド)距離が「ある値」以下の空間を n 次元球と呼びます。 「ある点」を球の中心、「ある値」を球の半径と呼びます。 なお、今回は球の 積み重ねられた立体の表面積:(前+右+上)×2 が成り立ちます。いちいちすべて計算しなくていいという事です。 出典:『塾技100算数』p94 問題)上記の立体がすべて1辺1cmだとしたら、表面積は? 積み重ねられた立体の表面積:(前+右+上)×2 答え




球台球带体积 侧面积 表面积计算公式与在线计算器 三贝计算网 23bei Com
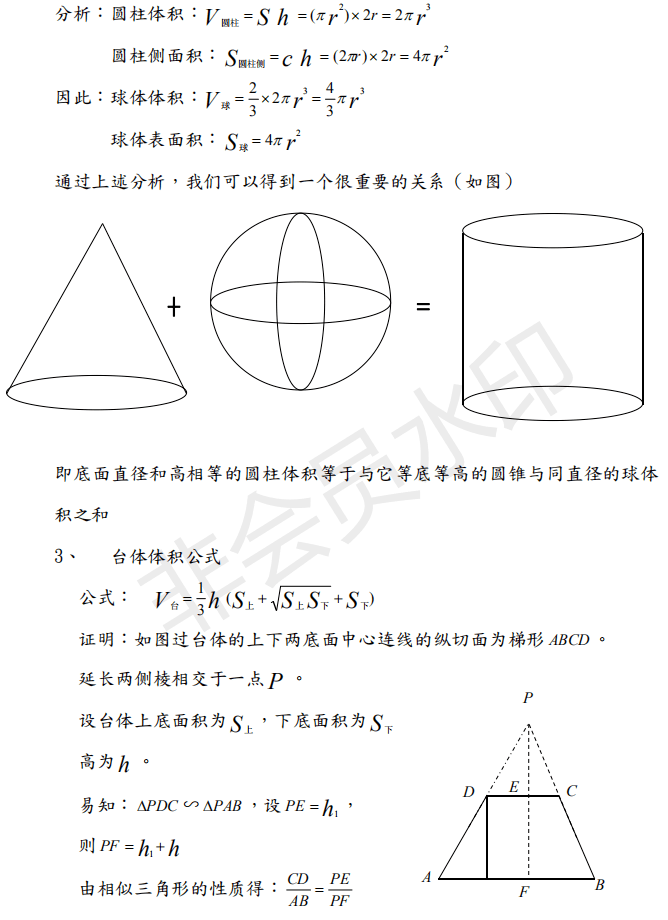
V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロンの公式 A = 面積 = bh/2 又は ヘロンの公式 jin弓形の回転体の体積と底面積と表面積を計算します。 一部が欠けた弓形の回転体の体積 一部が欠けた弓形の回転体の体積 弓形の回転体を切断した体積と表面積を計算します。 半球台の体積 半球台の体積 半球台の半径と高さから体積と表面積を計算します。以下の語呂合わせで覚える方法が有名です: 球の表面積: 4\pi r^2 4πr2 →「心配アール二乗」 球の体積: \dfrac {4} {3}\pi r^3 34 πr3 →「身の上に心配アール三乗」
球の表面積 < (2) 2つの比較 (1)(2)より, < 球の表面積 < 方法②:輪切りにする 指針(考え方) この円柱の側面積= 球の表面積の公式と同じ式をしていることが分かる. あなたは今、球の表面積を求める公式を知らないものとします. 円の面積は A = πr2 A = π r 2 円周は ℓ = 2πr ℓ = 2 π r 球の体積は V = 4 3 πr3 V = 4 3 π r 3 球の表面積は S = 4πr2 S = 4 π r 2 この式を見比べていて、中学生の時の僕は何か規則性があることに気づきました。 円の面積 A = πr2 A = π r 2 の式において、 r2 r 2 の 2 2 を Fusion360ボディの体積や表面積、質量や重心を求める方法 Fusion360で部品の体積や表面積、密度、質量、材料、慣性モーメント、重心等を確認する方法を調べてみました 何かと使う機会があるので覚えておくと便利です ボディごとや部品全体の要素を調べることができます
楕円体の体積 体積 V = 4π a b c /3 楕円体の表面積 (楕円面の表面積) a ≧ b ≧ c ならば、表面積は楕円積分を用いて次式で与えられる。小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題 こんにちは、ももやまです。 今回は2重積分を使って立体の体積や曲面積(表面積)を求める方法についてまとめています。 前回の記事(Part26)はこちら! 広義積分・ガウス積分についてまとめています。こ




表面積體積關係面積 表面積 體積 Vhjk




球扇形 球心角体 体积 表面积计算公式与在线计算器 三贝计算网 23bei Com
半径 r の球の表面積を求めよ。 解答 例5 例1の直円錐の表面積を区間0,rで求めよ。 解答 なお、体積Vは、V=1/3πr 3 例6 y=f(x)=r として例2にならい直円柱の表面積を区間0,lで求めよ。 解答 なお、体積Vは、V=πr 2 l面積 メンガーのスポンジの次元は2より大きいため、2次元的な大きさである 面積 は無限である。 表面積が1となる大きな立方体から穴を空けてメンガーのスポンジを構成する場合、一度目の穴を空けると、その表面積は 1 3 {\displaystyle {\tfrac {1}{3}}} 増加する。 表面積 S = ∞ → 無限 体積 V = π → 有限



圆锥表面积公式 圆锥表面积与体积 图文 叽叽歪歪吧




圆环体的体积和表面积怎么算 知乎
体積・表面積 算数 中学数学 空間図形 立体の 体積の求め方(公式) を一覧にまとめました。 公式を忘れてしまったときには、こちらで確認しましょう。 体積の求め方公式 立方体・直方体の体積の求め方 円柱の体積の求め方 三角柱の体積の求めその体積は (「体積比は相似比の3乗比」を使えば,相似比が1:2だから体積比は1 3 :2 3 =18 が求まる.) 球の表面積 半径 r の球の表面積を S で表わすと S=4πr 2 (解説) 底面積を S ,高さを h とするとき,三角錐,四角錐,・・・,円錐の体積は楕円体の体積 腎臓の大まかな体積の確認目的。 楕円体形状の腎臓動脈瘤の塞栓で、使用するコイルの適合サイズを表面積で推測するのに使用しました。 大変役に立ちました。 ありがとうございました。 学校の宿題に使いました。 ありがとうござい



表面积体积公式大全 搜狗图片搜索




圆环体体积 表面积计算公式与在线计算器 三贝计算网 23bei Com
体積と表面積1 平面図形 (角度)13 体積と表面積2 平面図形 (角度)14 体積と表面積3 平面図形 (角度)15 体積と表面積4Hello School 算数 体積・表面積 練習問題 解答と解説 インターネット上で受験算数の一通りの基本的解法をマスターしよう♪。 ※特に指定がない場合、円周率は314とします。電話番号:02 ファックス番号:02 メールでのお問い合わせはこちら 村民のまめな暮らしガイドブック くらしの相談窓口 便利な電話番号 年齢早見表(19年用) 鮫川村の郵便番号 度量衡換算表 (長さ・面積・体積・重量) 県南地域の県立



7 3球的表面积和体积 北师大版高中必修2数学电子课本 数九网



长方体的表面积和高中初中 的体积学自己信网查到可以 公式 高中课题目
⚠ 4:円錐の体積に関する練習問題 この章からは、円錐の体積、表面積に関する問題を解いて見ましょう! まずは円錐の体積に関する問題からです。 問題 下の図の立体についてそれぞれ求めなさい。 9②球の表面積の公式の求め方(1) 次に、球の表面積の公式の求め方について考察する。 まずは体積のときと同様にすると、図1において、 球の中心から距離 x の点で切った断面である円の 円周の長さは、 2 -x 2) となる。 よって、球の表面積Sは、円周を x47 7 立体の体積と表面積 133 次の図の直方体の体積と表面積を求めよ。 ⑴ ⑵ ⑶ 137 次の図の立体の体積と表面積を求めよ。 ⑴ ⑵ 135 次の図の円柱の体積と表面積を求めよ。 ⑴ ⑵ ⑶ 134 右 の図は ,円柱とその展開図である。 次の問いに答えよ。



正方体的表面积和体积公式是什么正方体的表面积和体积公式是怎样的 天奇生活
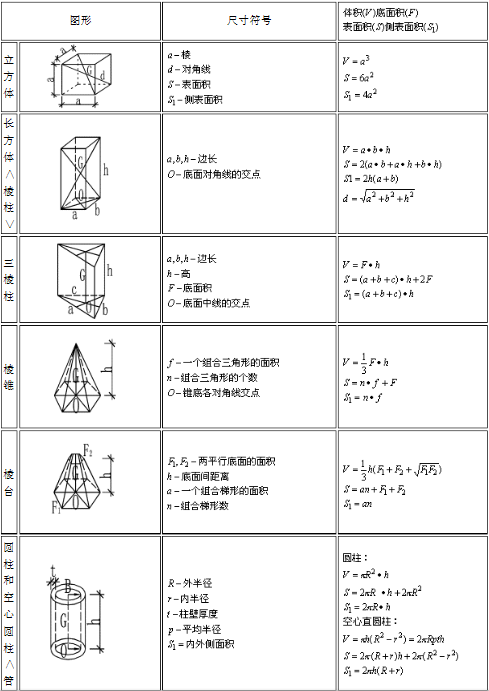



建筑类计算 多面体的体积和表面积开源地理空间基金会中文分会开放地理空间实验室
球の半径を入力 r = 10 球の体積 V = 球の表面積 S = ここでは半径「10」の球の体積と表面積を計算してみました。 その他のサンプルプログラムも合わせてご覧ください。 C言語のサンプルプログラム集(体積の計算) 立体の体積を求めるには,体積の微分が断面積になることを利用します. すなわち,左端 a から座標 x までの区間にある体積を x の関数として V(x) で表し, x における断面積を S(x) とおきます. 上で復習した面積の求め方と同様にして




Ppt 體積與表面積powerpoint Presentation Free Download Id



表面积体积公式大全 搜狗图片搜索




求球体的表面积和体积 修也 Csdn博客



圆锥体积公式的由来 圆柱圆锥常用的表面积体积公式 尚书坊




15六年级数学下册圆柱表面积 圆锥体积练习题 Doc 文档分享网



五年级数学下册 长方体和正方体 掌握表面积体积容积计算 学习视频教程 腾讯课堂



五年级下册 图形的表面积和体积练习题一 松鼠文库



空間幾何體的表面積和體積講解及經典例題 上 雪花新闻



简单几何体的表面积与体积ppt免费下载 第一ppt




鴻隼企業有限公司 一分鐘了解比表面積 Q 什麼是比表面積 Specific Surface Area A 比表面積 指的是多孔固體物質單位質量所具有的表面積 維基百科 更簡單來說 如圖從一個邊長10公分的立方體 將它切割成邊長1公分的立方體時 其總表面積瞬間從600平方公分



圆锥侧面积表面积体积公式 圆锥体积表面积公式 公式学习



三棱锥体积公式 四棱台表面积公式 尚书坊
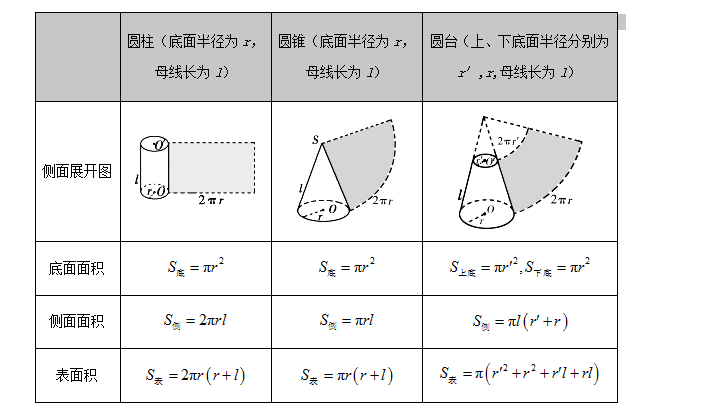



高考数学考点之空间几何体的表面积和体积 王羽课堂



空間幾何體的表面積和體積講解及經典例題 上 雪花新闻








體表面積計算表面積 Sylgf




圆柱圆锥常用的表面积体积公式 豆知网



Q Tbn And9gcrb4blzi9vddmsv6c33dfu2ymwljv9pqvinxvz2heat Qlxblsn Usqp Cau
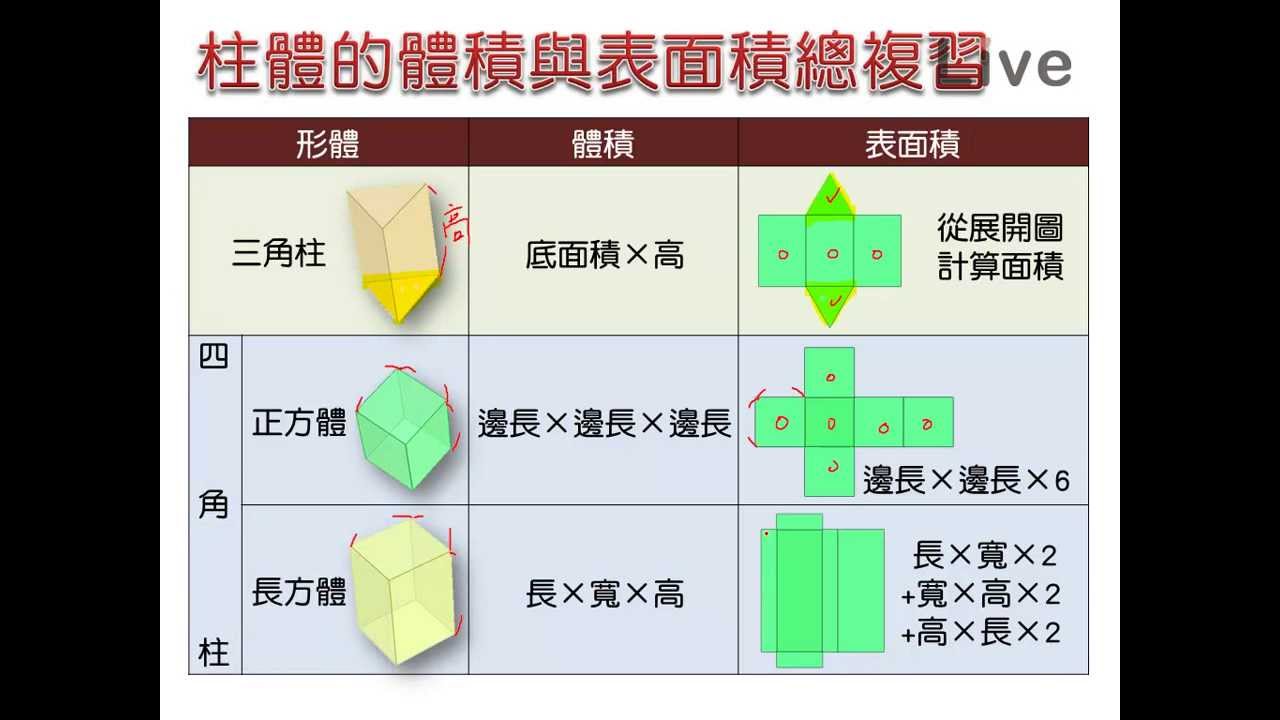



7 國小數學總複習 圖形 體 體積與表面積 觀念 By Live數位國中數學 名師葛倫 Youtube




錐體體積公式



看图计算物体的表面积与体积 题目和参考答案 青夏教育精英家教网



圆柱体积与表面积对比精选测试 松鼠文库




圆锥体体积 表面积 质量在线计算器 三贝计算网 23bei Com




体积和表面积 练习 3d动画 Mozaik电子教育与学习



22高三数学第一轮复习 空间几何体的表面积与体积公式大全 整理



多面体体积与表面积 文档库



小学数学奥林匹克竞赛真题精选五年3 长方体体积与表面积 哔哩哔哩 つロ干杯 Bilibili



圆环的体积公式是什么圆形的面积表面积体积公式是什么 学习岛
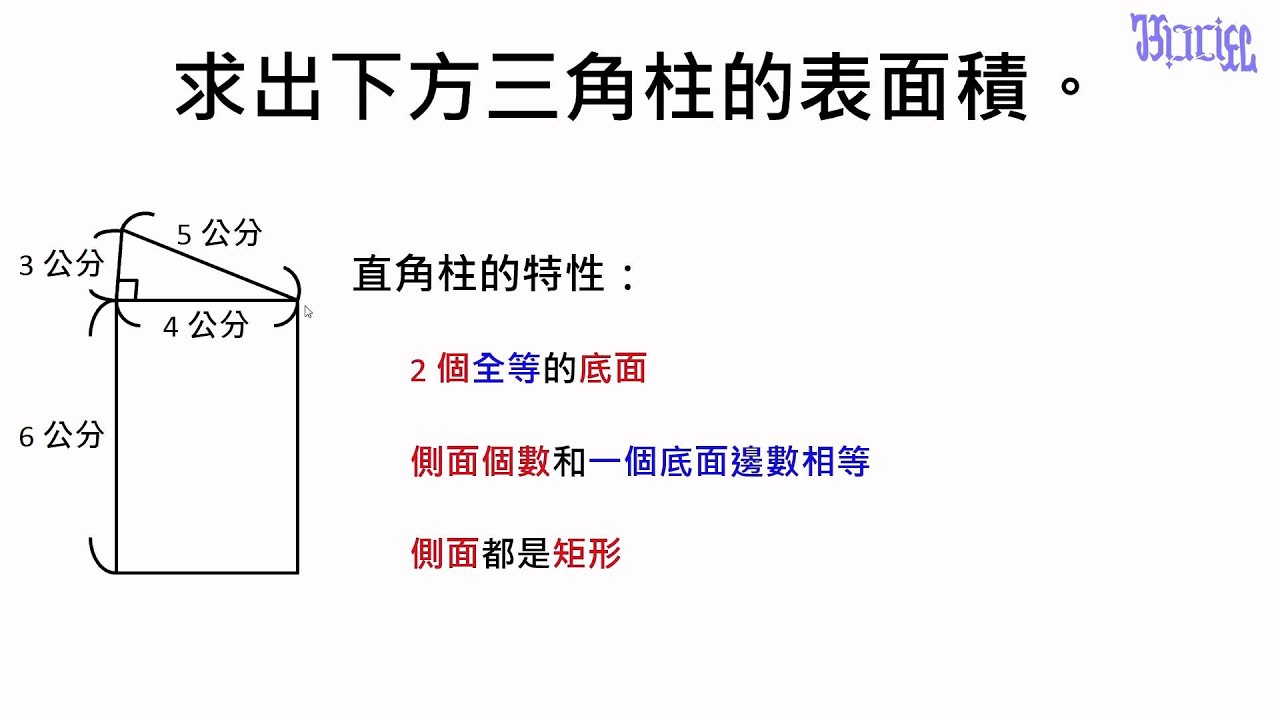



柱體的體積與表面積 03 求出三角柱的表面積 Youtube




各類幾何體的體積與表面積的計算問題 每日頭條
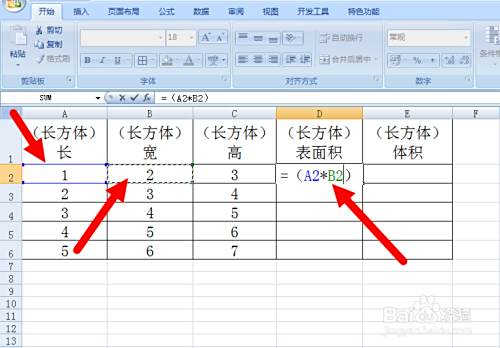



用电子表格求长方体的表面积和体积 百度经验




长方体正方体的表面积和体积练习 Ppt



微积分计算球的表面积如何推算出球的表面积
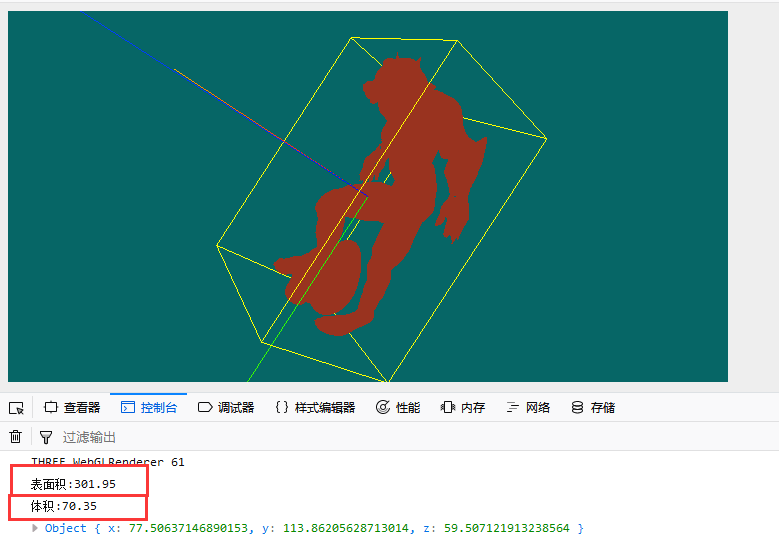



3d模型展示以及体积 表面积计算 Solo李 博客园




表面积和体积的区别 解历史




球的表面积例题 球的表面积和体积公式是什么 三人行教育网 Www 3rxing Org




表面积 Surface Area 和体积 Volume 的区别 Tl80互动问答网



正方体的表面积与体积计算问题 哔哩哔哩 つロ干杯 Bilibili




高考数学考点之空间几何体的表面积和体积 王羽课堂
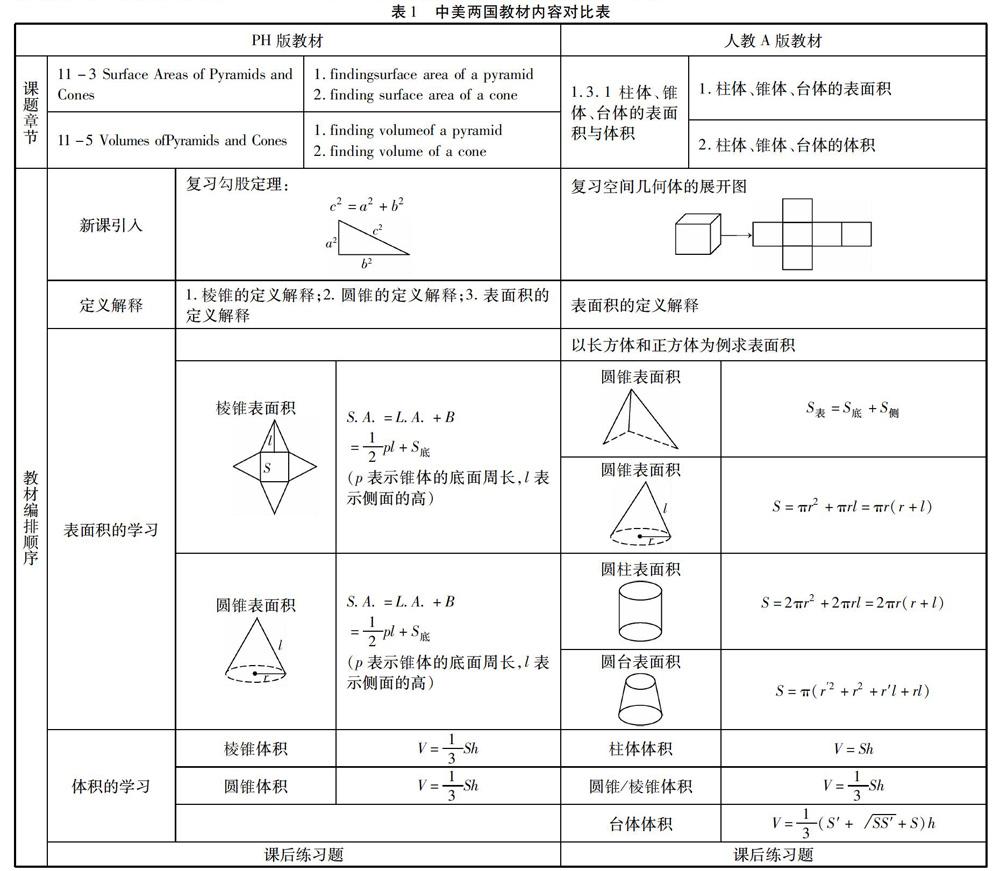



锥体的表面积与体积 中美教材对比 参考网




14 平面及立體圖形 立體圖形的表面積及體積 齊齊溫




球台球带体积 侧面积 表面积计算公式与在线计算器 三贝计算网 23bei Com



球的体积求导便是球的表面积 互为逆运算 降维与升维 五四公社
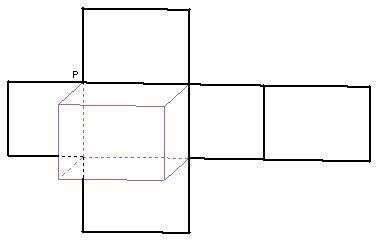



高中数学 空间几何体的表面积和体积 楠木轩




呆哥数学立体几何 表面积与体积 常考例题分析 2 知乎



圆球体积公式 球的体积和表面积 趣闻趣事网



1



圆锥表面积公式体积 万图壁纸网



Q Tbn And9gcrb4blzi9vddmsv6c33dfu2ymwljv9pqvinxvz2heat Qlxblsn Usqp Cau




盒子表面的秘密 表面積 快樂是自找的 痞客邦




长方体 正方体的表面积与体积 知识精要 典型例题 模仿练习 每日头条




面積 表面積 體積的比較 宣宣 2013 の部落格 隨意窩xuite日誌




立体图形体积和表面积计算的知识梳理
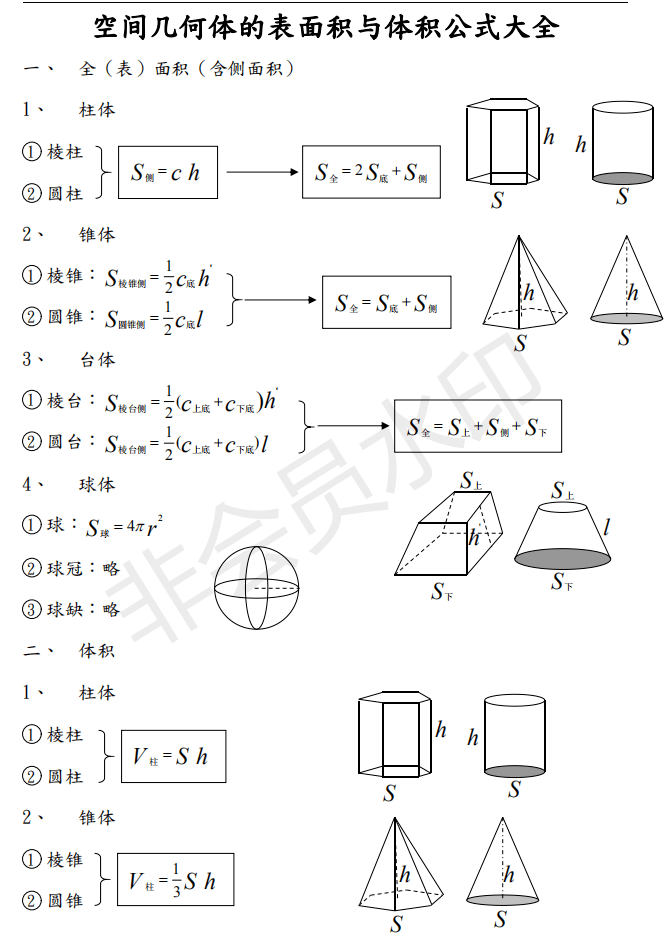



22高三数学第一轮复习 空间几何体的表面积与体积公式大全 整理




基礎 長方體邊長縮放後的體積與表面積 Youtube




正方体的表面积公式是什么 长方体和正方体棱长和 表面积 体积计 豪友网




柱体体积公式 新人首单立减十元 21年8月 淘宝海外




球的表面积与体积 怎么用微积分证明球的表面积和体积公式 三人行教育网 Www 3rxing Org



小学五年级奥数练习题 体积和表面积 面积计算 奥数网




球的体积 表面积 简书




用白色粉笔 在黑板与数学公式的总表面积 体积 空间对角线的几何形状方柱体插画 正版商用图片0z5ygw 摄图新视界




球帽球体积球楔比表面积 点公式png图片素材免费下载 图片编号 Png素材网




球的表面积和体积怎么算啊怎么计算球的表面积



备考复习空间几何体的表面积与体积高考命题方向 问题



五年级数学 长 正方体 体积和表面积例3 哔哩哔哩 つロ干杯 Bilibili




正四面积体体积 表面积计算公式与在线计算器 三贝计算网 23bei Com



怎么算表面积和体积 西瓜视频搜索
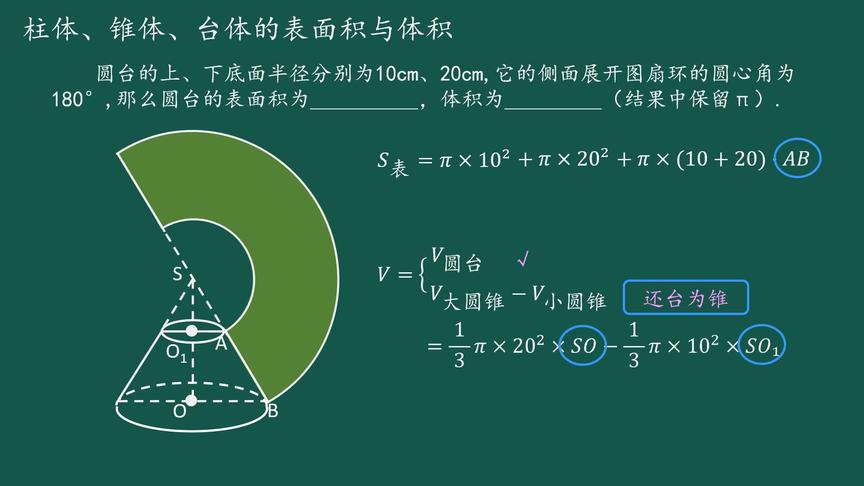



圆台的表面积体积公式 西瓜视频



高中数学空间几何体的表面积和体积讲义




简单几何体的表面积与体积 立体几何初步ppt 球的体积和表面积 下载 牛二ppt



圆球体积公式 球的体积和表面积 趣闻趣事网




Matlab函数脚本function计算正方体体积和表面积 百度经验



正方体的表面积和体积公式是什么正方体的表面积和体积公式是怎样的 天奇生活



圆环的体积公式是什么圆形的面积表面积体积公式是什么 学习岛




体积相同的球体和正方体 哪个表面积大球体积 表面积公式是




球体表面积公式 球体体积公式 环球信息网




棱镜体积表面积矩形公式 数学png图片素材免费下载 图片编号 Png素材网



初中长方体的体积公式和表面积公式 初三网



体形面积所有图形的面积体积表面积公式 女士吧




高中数学必修二经典考题 球的表面积和体积 含答案 三好网



图形公式大全表面积 万图壁纸网



立体图形的表面积和体积的计算方法及公式 立体图形的表面积和体积 奥数网



1



五年级数学下册 长方体和正方体 掌握表面积体积容积计算 学习视频教程 腾讯课堂




长方体表面积体积立方体png图片素材免费下载 图片编号 Png素材网




體表面積表初中數學 幾何 面積與體積公式 Uhlwc



体积公式大全所有图形的面积体积表面积公式 尚书坊




圆锥体积公式 新人首单立减十元 21年8月 淘宝海外



小学生对长方体 表面积 体积 理解现状及空间观念培养研究




圆柱体积公式和表面积公式是什么 星火网校



如何在rhino中计算复杂几何模型表面积与体积




周长 面积 表面积和体积 3d动画 Mozaik电子教育与学习
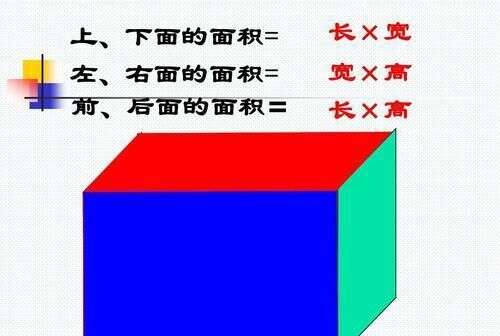



小学数学知识点 长方体与正方体的表面积与体积 楠木轩




长方形的体积公式字母表面积公式怎么计算公式 小街网



0 件のコメント:
コメントを投稿