証明問題など/底辺比と面積比など/相似比と面積比/ 相似比と体積比など /FdData 入試製品版のご案内 FdData 入試ホームページ掲載のpdf ファイル(サンプル)一覧 ※次のリンクはShiftキーをおしながら左クリックすると,新規ウィンドウが開きます 理科: 理科1 年,理科2 年,理科3 年の相似条件,平行線と 線分の比についての 性質,相似比と面積比 及び体積比の関係な どを理解し,知識を身 に付けている。 4 単元について (1) 単元について 学習指導要領の第3学年の目標(2)に「図形の相似,円周角と中心角の関係や三平方の定理相似比が5:3 のとき,面積比は52:32=25:9 となる。 問題(2 学期期末) 2 つの相似な図形で,相似比が7:3 のとき,次の各問いに答えよ。
相似比の利用 三平方の定理 無料学習プリント教材
相似 面積比 応用問題
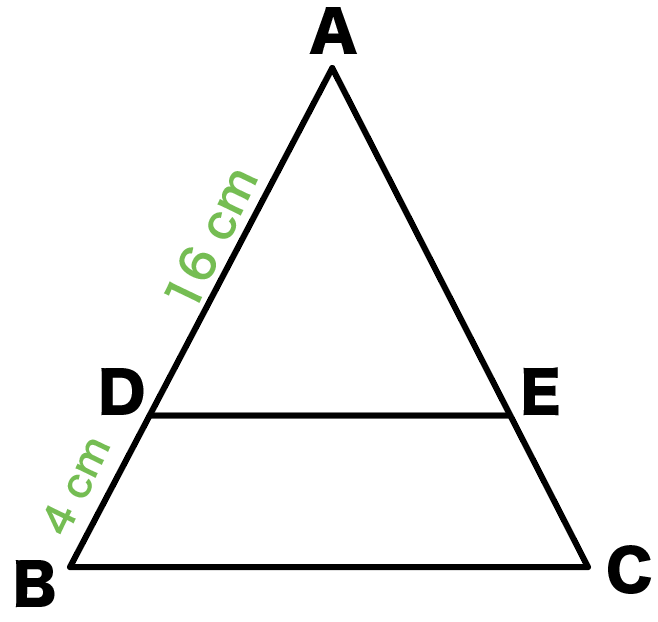
相似 面積比 応用問題-・相似比 24:36=2:3 ・面積比 22:32=4:9 ・Lサイズの値段をx 円 4:9=:x 今日は,この相似比や面積比が日常生活のどんなところで 役に立つのか考えましょう。 次の問題に取り組みましょう。 あるピザ屋では,ミックスピザの値段が,相似と面積比 図で、ADDB=AEEC=21である。 台形DBCEの面積を求めよ。 BC=10cm, ADEの面積は16cm 2 である。 EBCの面積を求めよ。 台形ABCDの面積を求めよ。 BC=cm, AEEB=DFFC=23である。 EFの長さを求めよ。 台形AEFDと台形EBCFの面積比を求めよ。




平面図形をマスター 三角形の面積比 応用編その3
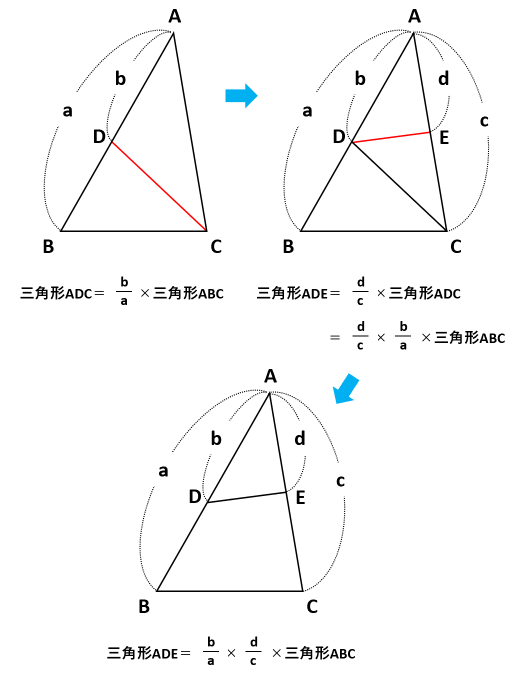
数学35章図形と相似「相似な図形」<基本問題①> 組 番 名前 A B C E (1)辺BCに対応する辺を答えなさい。 (2)四角形ABCDと四角形EFGHの相似比を求めなさい。 (3)辺EFの長さを求めなさい。 A D B C 60° 6cm 8㎝ E H F G 80° 6cm前回までは、相似の応用問題を中級レベルのテストから選び、 「小問ごとに図を書く」 というテクニックで攻略できることを見てきました。 そこで今回は、 難度の高いテスト に出題された, 相似を中心とした「辺の比と面積比」の問題について、 このテクニックが通用するかについて調べていきます。 まずは、サピックスのオープンテストからの問題です。 13 (3) と の面積比を求めなさい。 まず相似であることを求めます。 相似の証明は相似の問題の解法の応用問題(2)をご参照ください。 次に相似比を求めます。
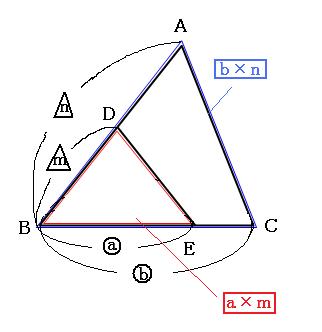
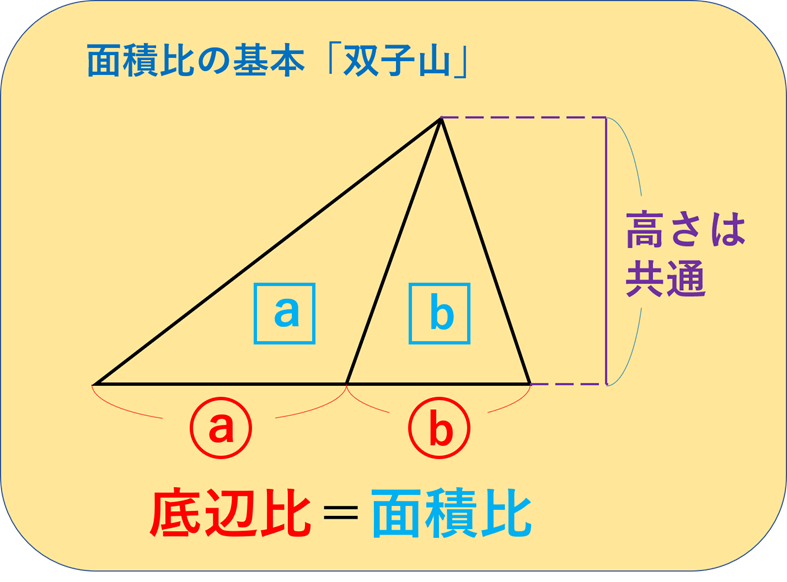
練習問題1 以下の面積比を最も簡単な整数の比で表しなさい。 1 相似比が2:3である三角形アとイの面積の比 相似比が2:3なので、 面積比は、2 2 :3 2 =4:9 ≪答≫ 4:9相似比を用いて解決する身近な教材の研究と実践 鷲見浩章 1,愛 」という問題(以下,問題 P と記す)を考える。金華山とは,岐阜市に のように相似の応用とした方が証明も必要と なるので,この扱いの方が適切であると考え た。また,5では,同じように相似を用いた 証明が紹介さ 相似比から面積比を求める考え方はよく使うので、しっかり理解しておきましょう。 三角形の相似 ここからは、問題として最も多く使われる三角形の相似について詳しく見ていきましょう。 三角形の相似条件
相似図形をさがす問題 ※ 分からないとき → とりあえず「これだ」と思う答を選べば正誤にかかわらず「ヒント」ボタンが出ます.正答のときでもヒントから得られるものがあるかもしれませんし,誤答のときでもヒントを見なくてもかまいません. 相似比と面積比 相似な図形の面積比の問題です。 基本を確認して、いろいろな応用問題を解けるようにしてください。 基本事項 相似比が m n である図形の面積の比は, m2 n2 である。 例)下のような相似な三角形がある A 応用になるとX型の問題が多くなります。 というよりも、A型でもX型でもできる問題は、単純なX型の方が解きやすいので、X型を使うことを推奨しているという意味です。 興味のある方はこちらにどうぞ 対話式算数とは 小5対話式算数 第75話:相似①の概要 75・1 A型の相似です。 2



相似比と底辺比から面積比を求める 基準となる三角形を探せ みみずく戦略室



面積が何倍かを求める問題 応用編 苦手な数学を簡単に
相似 応用学習 図形で比を使いこなせ 応用学習 相似を見抜こう 添削問題 添削問題1 添削問題 添削問題2 この教材見本は、実際の1カ月分の教材よりも回数・ページ数が少ないダイジェスト版です。 巻末 添削指導例 4要点4 30分 要点学習相似 要点 相似比と面積比・体積比の関係 1STEP 1 : A D O ∽ C B O A D C B = 12 c m c m = 3 5 (相似比) POINT:対応する線分の長さの比は、すべて等しい STEP 2 : A E O ∽ A B C ( B E O ∽ B A D でもOK) ③ ③ ⑤ A O A C = ③ ③ ⑤ = 3 8 (相似比) 3 8 = a これを解いて、 a = 15 2 STEP 3 : D F O ∽ D C B 同じように 応用問題が解けなくなります。 ★★★ download ここでは、「相似形の面積比の基本(面積比は相似比の2乗)」と「台形ペケポン」を習います。「台形ペケポン」とは、(台形を2本の対角線で区切って面積比をかきこむ問題で、面積と比の単元では頻出問題です。このプリントで沢山練



中3数学相似な三角形の面積比の応用の問題がわかりません 解き方を読ん Yahoo 知恵袋




高校入試対策数学 面積比に関する対策問題 Pikuu
相似分野の応用問題①ラスボスっぽいの,多分それ連比です。 面積の比 (何倍)を求める問題も含めてかんたんな方法を解説します 教遊者 If playback doesn't begin shortly, try restarting your device Videos you watch may be added to the TV's watch history and influence TV recommendations To avoid this, cancel and sign in to on your computer 難関中学に合格する!!相似形と面積比・図形の移動トレーニング 入試によく出る図形問題100問 中学受験 算数脳を鍛える!! 改訂3版 (YELL books 賛数仙人の教え)/井上 慶一(教育・学習参考書) 図形の面積比や移動に関する問題を、基本問題から応用問題まで、大事な問題、入試に基本的な応用です。???? 17年9月16日 相似比と面積比についての練習です。かなり基本的な話です。 苦手な人向けです。 次回追加分は面積について計算していくものになります。 17年9月12日 画像にあるような三角形の相似に関しての長さを求める問題です。 台形については、補助線がポイントです。難易度ちょい上がりますが、いずれも基本的な内容と思い



相似図形 高校入試問題
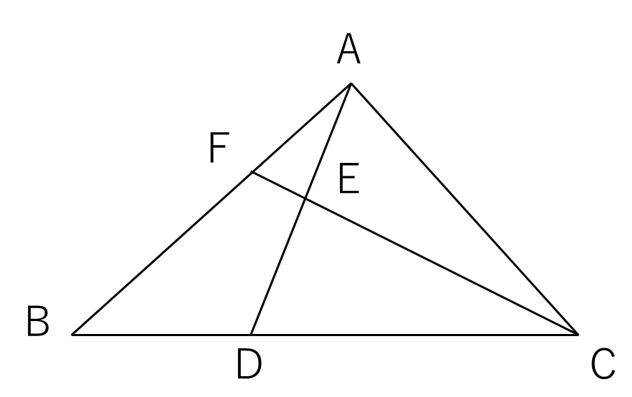



三角形の面積比をてんびんで解く 中学受験プロ講師ブログ
さらに,相似な図形の相似比と面積比,体積 比の関係など相似な図形の計量に関する学習を通して,相似な図形の理解をさらに深めるとともに, 数学のよさを体験させながら数学的な推論に関する能力,図形について見通しをもって論理的に考察 する能力を伸ばしていきたい。 (2) 生徒観 本 苦手な生徒が多い「面積比」の問題。 その解法のポイントを、全6回にわけて解説していきます。 前回の記事 ⇒ 最重要パターン‟高さ共通"と"相似" 早速、例題を見てみましょう。 台形abcdがあり、上底adと下底bcの比は2:3です。 台形の面積が50cm 2 であるとき、 aobの面積はいく図形の問題の組み合わせ。 相似比と面積比。 理解して押さえていないと苦しいと思うんだけどな。 まずは解答。 一行目に「⊿ADP∽⊿EBPだから」とあるけれど、まず解答でこの三角形の相似に着目したことがすんなりと理解できるだろうか? 説明できる
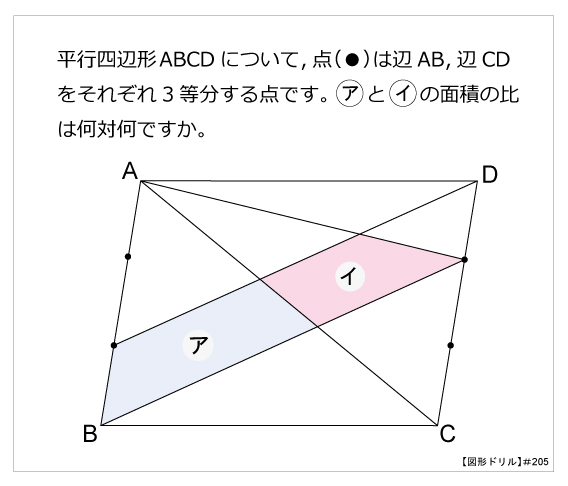



平行四辺形 算数星人のweb問題集 中学受験算数の問題に挑戦




面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学
正六角形と線分比・面積比の応用問題です。 台形の相似 一度ははっきりと確認しておきたい,台形の相似に関する問題です。 正十角形と正二十角形 正多角形の面積の関係に関する,シンプルな問題です。 正三角形のマス目における長方形 正三角形のマス目上でいろいろな長方形を作る問題つまり pef∽ pbcの面積比は1692=13 217 2 よって相似比は1317 bc=17なのでef=13 学習 コンテンツ 練習問題 各単元の要点 pcスマホ問題 数学の例題 学習アプリ 中1 計算問題アプリ 方程式 中1数学の方程式の計算問題を徹底的に練習 相似・線分比と面積比の徹底演習65問 相似・線分比と面積比の徹底演習65問 算数徹底演習 中学受験算数の「相似・線分比と面積比」を完璧にするために、全65問の演習プリントを作成しました。 3レベルに分けてありますが、レベルAが必修問題、レベルBがR4や四谷でSS55程度の中堅校、レベルCが難関校レベルになります。 目次 1 PDFファイル(問題



すぐるゼミ 相似な図形の応用
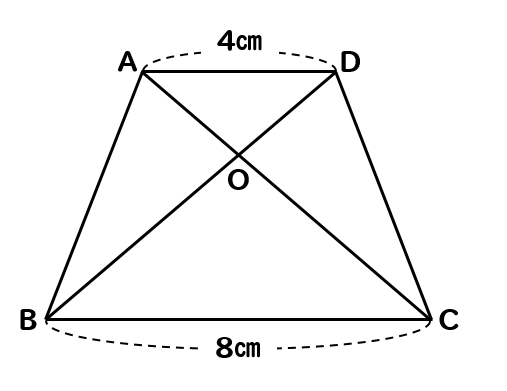



相似 台形と面積比の問題を徹底解説 数スタ
相似比の練習問題(平行四辺形1) 問1. (ア) (1) EFD ∽ CFB よりED:CB =EF:CF =1:3 CFD の面積=2 ×3 =6cm2 (2)BF:FD =3:1 より BCF の面積=6 ×3 =18cm2 or EFD ∽ CFB より相似比1:3 →面積比1:9 2 ×9 =18 cm2 (3) ABCD の面積=(6 +18)×2 =48cm2 (イ) 相似な図形の面積比の問題です。基本を確認して、いろいろな応用問題を解けるようにしてください。基本事項相似比が m n である図形の面積の比は,m2 n2 である。例)下のような相似な三角形がある ABCと A'B'C'の相似比は 1:2面積を求めると ABC=4 A'B'C'=16 面積比は1:4相似比が1:2のとき面積比は 12 22 となる。*立体の表面積の比も立体の相似比がmDJBは相似で相似比は3:2。 また、三角形ECDと三角形EAB は相似で相似比は1:2。 よって、AB=16cm。 三角形FGJと三角形FHBは相似 で相似比は1:2。 よってGH=8cm。 求める面積は(816)×8÷2=96cm 2 。
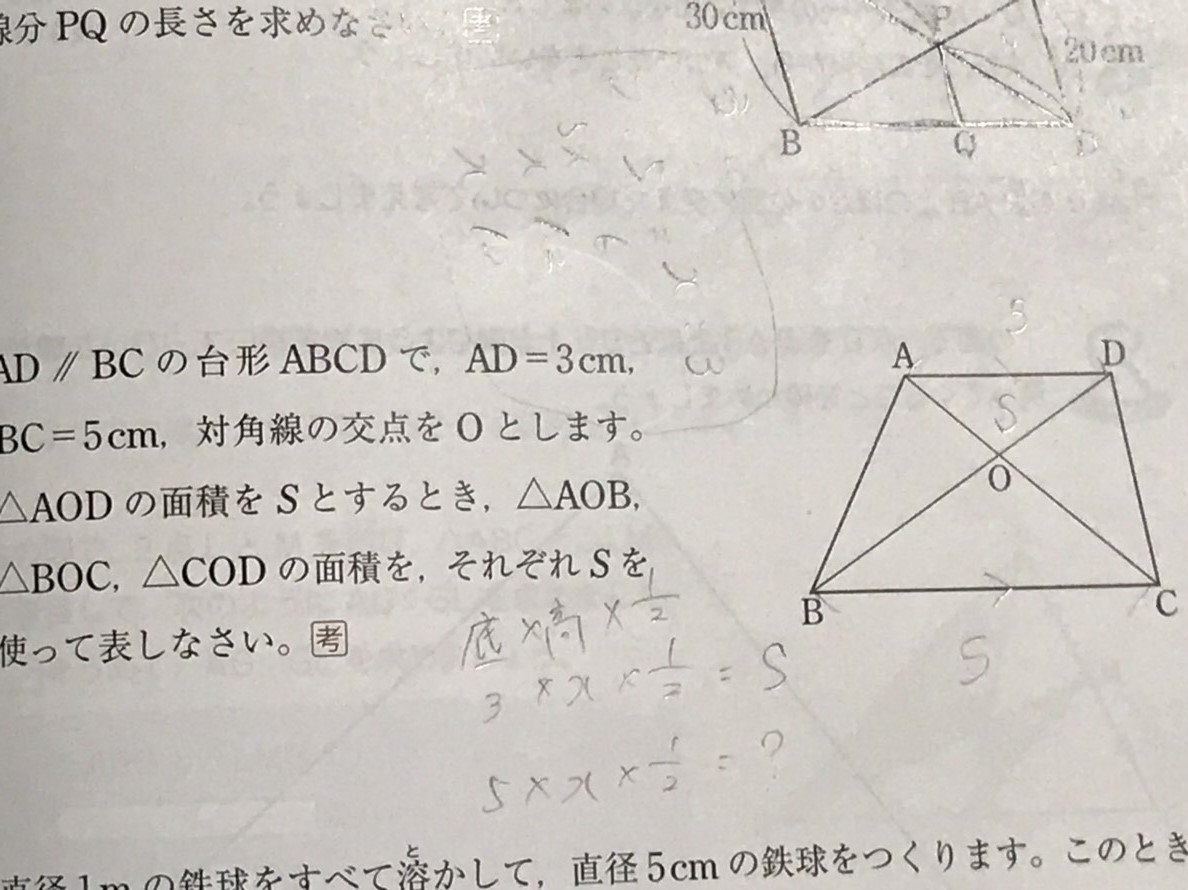



面積比



3
図形と相似の最終回です。 計算に関する問題が中心となりますが、 特に面積比・体積比はしっかりと練習しておきましょう。 11.角の二等分線と線分比 eclus13 215K subscribers Subscribe 角の二等分線と線分比 中3数学 図形と相似11苦手の克服 相似2 Tweet 図形の練習問題 | 16年08月日18時00分 「第301回 苦手の克服 相似2」 今回も、相似を中心とした、「辺の比と面積比」について、 苦手の克服を考えていこうと思います。 前回同様、 「相似が2組ある問題」「相似とそれ以外の 面積比の問題で扱う図形にはいくつかの"型"がありますが、それらが頭の中できちんと整理されていないと、考え方の手順がなかなか浮かんできません。 今回の連載では、受験で登場することの多い6つの型を取り上げます。 症状② "比の扱い"が不慣れ 面積比の問題の多くは、「比の合成



面積と辺の比の関係を解説 図形の面積と辺の比の関係はテントやドリルで面積を求める
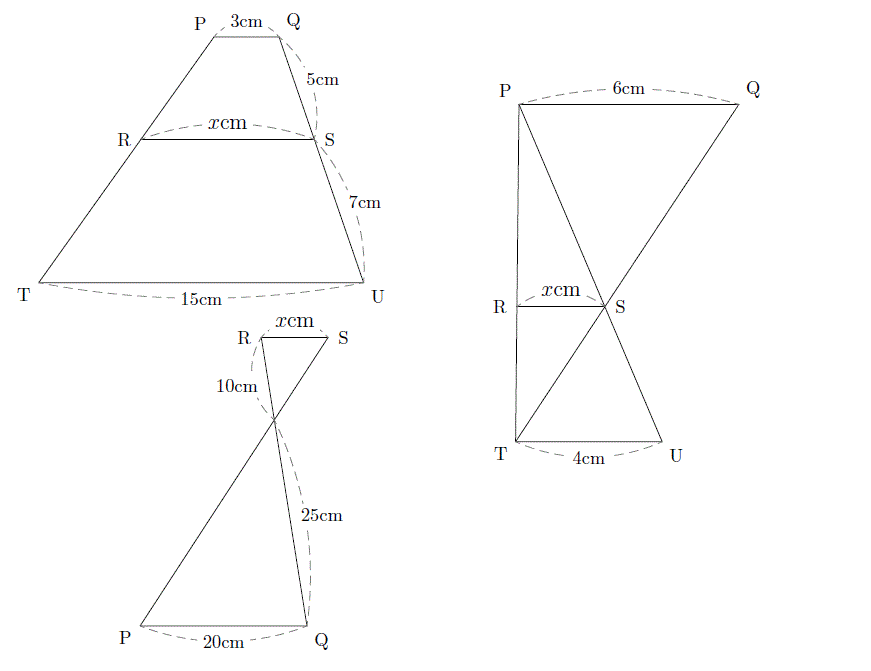



かみのドリル 相似
★ ⑶ aeh と平行四辺形 abcd の面積比を求めよ。 4 次の問いに答えよ。 ⑴ 図1の abcd で,ae:eb=2:1 のとき, aeg と dfg の面積比を求めよ。 〔和洋国府台女子高〕 ⑵ 図2の2つの三角錐 o ‒ abc と o ‒ def は相似で, 図形問題への応用を念頭に置いているので厳密さよりもわかりやすさを重視しています。 → 複比の定義と複比が不変であることの証明 調和点列の様々な定義と具体例 調和点列: 同一直線上に四点 a, p, b, q a,\p,\b,\q a, p, b, q がこの順にあるとき, 1: a p p b = a q q b appb=aqqb a p pb = a q qb中点連結定理を使った問題を解説! 相似の面積比を求める問題をイチからやってみよう! 面積比!平行四辺形の面積問題を解説!←今回の記事 面積比!台形の面積比問題を解説! 円錐の体積比を解説!



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ



3
相似比と面積比,体積比の公式の証明 レベル ★ 基礎 平面図形 更新日時 相似な平面図形について,面積比=相似比の二乗 相似な空間図形について,体積比=相似比の三乗 面積比をきちんと理解できれば体積比もほぼ同様に理解できるので相似比と面積比の基本問題 長さは?(城北中学 11年) 工夫の一手は?(西武学園文理中学 10年) 面積比と台形の面積(神奈川大学附属中学 10年) 面積比と面積(東海中学 09年) 光源と影(聖光学院中学 10年) 今年出題された図形問題(西大和学園中学 12年) 難問に挑戦(第11回



相似分野の応用問題 ラスボスっぽいの 多分それ連比です 面積の比 何倍 を求める問題も含めてかんたんな方法を解説します 教遊者
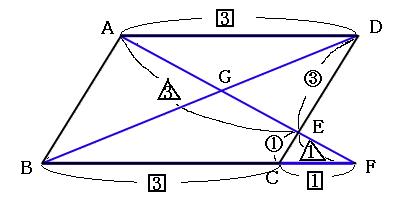



平行四辺形の対角線を3つに分ける問題を解くときはチョウチョを2匹探せ



Math 空間図形と相似 面積比 体積比 発展問題 働きアリ
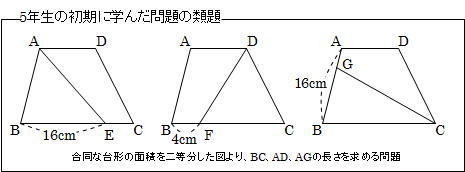



小5の学習ポイント4 辺の比と面積比 前田昌宏の中学受験が楽しくなる算数塾




平面図形をマスター 三角形の面積比 応用編その3




中3数学 相似 台形の対角線 Youtube




大至急です 相似 面積比の問題です Clear




相似 平行四辺形と面積比の問題を徹底解説 数スタ




平面図形をマスター 三角形の面積比 応用編その3




相似比の利用 三平方の定理 無料学習プリント教材




中3 数学 6 7 相似比と面積比 平行四辺形 Youtube




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
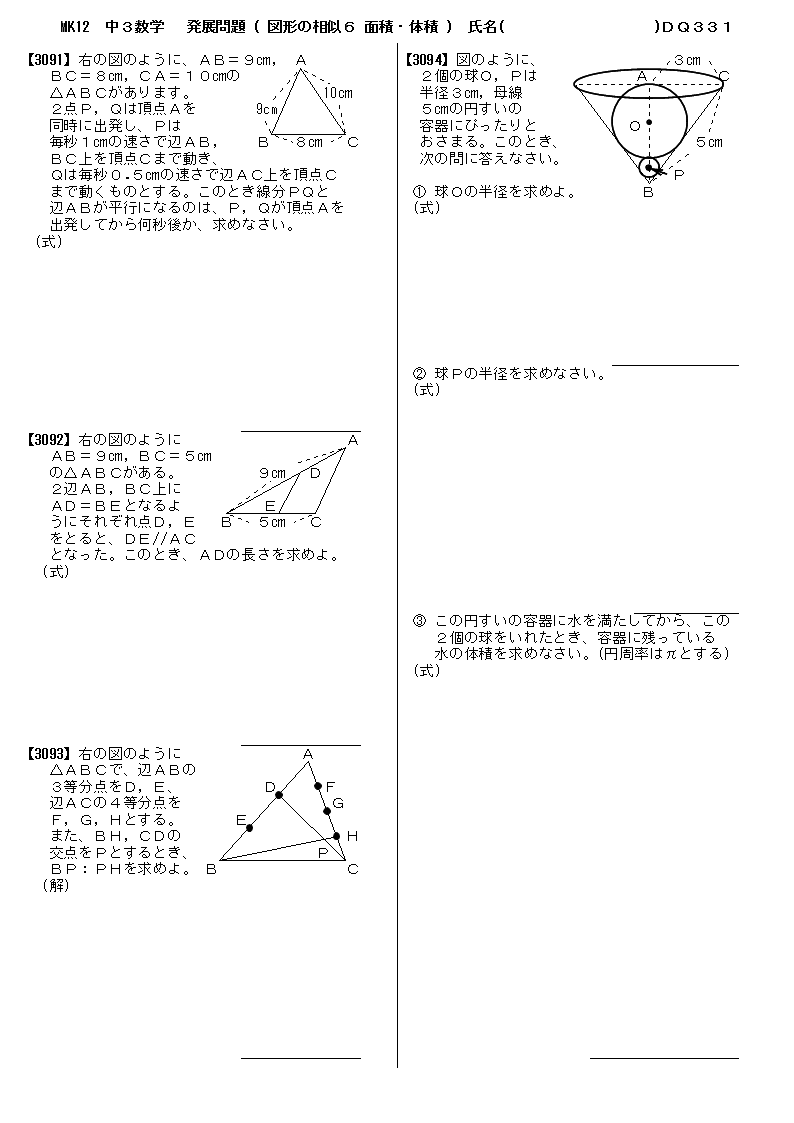



無料 中3数学 発展 応用問題 問題プリント 331 図形の相似6 面積比 体積比




面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学



みんなの算数オンライン 中学受験6年 平面図形 実戦過去問 応用




世界一わかりやすい数学問題集中3 5章 図形と相似



中3数学12 図形の相似3 線分の比 発展問題プリント 問題 328




平面図形をマスター 三角形の面積比 応用編その2




平面図形をマスター 三角形の面積比 応用編その3




中3数学 相似な図形の面積比 練習編 映像授業のtry It トライイット




これでバッチリ 相似の面積比を求める問題をイチからやってみよう 数スタ



これでバッチリ 相似の面積比を求める問題をイチからやってみよう 数スタ




補助線の引き方 日々の学習 兄中学受験




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく




相似な図形 補助線を引いて考える相似の問題 中学生からの勉強質問 数学 進研ゼミ中学講座



Math 空間図形と相似 面積比 体積比 発展問題 働きアリ



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ




相似の面積比を求める問題 上級編 Youtube



平面図形 直角である必要はないのだ




難関中学に合格する 相似形と面積比 図形の移動トレーニング 入試によく出る図形問題106問 中学受験 算数脳を鍛える 増補改訂4版の通販 井上 慶一 紙の本 Honto本の通販ストア
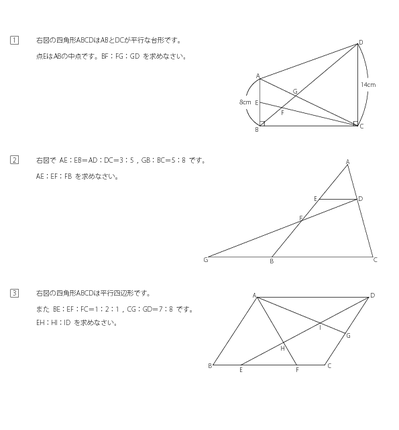



みんなの算数オンライン 中学受験5年 相似比と面積比3 相似の利用1



Studydoctor相似比と面積の計算 中学3年数学 Studydoctor
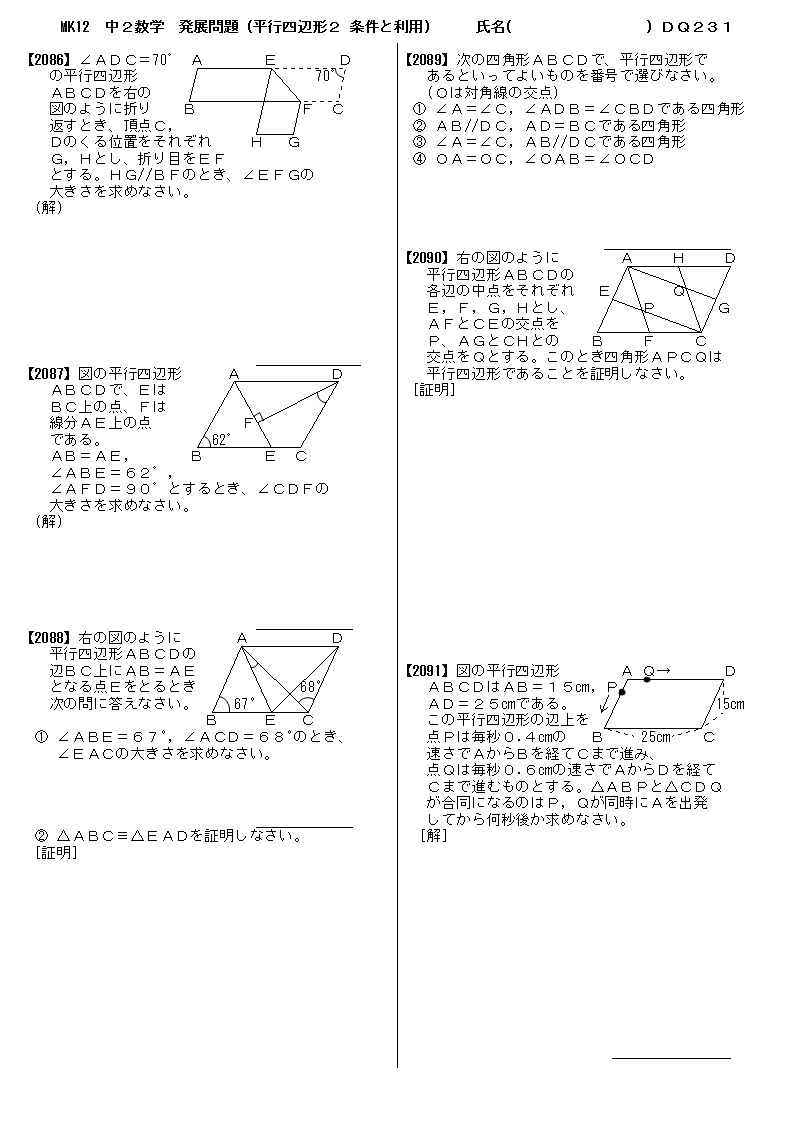



無料 中2数学 応用 発展問題 問題プリント 331 図形の相似6 面積比 体積比




平面図形をマスター 三角形の面積比 応用編その3




相似比と面積比 無料で使える中学学習プリント




相似分野の応用問題 ラスボスっぽいの 多分それ連比です 面積の比 何倍 を求める問題も含めてかんたんな方法を解説します 教遊者
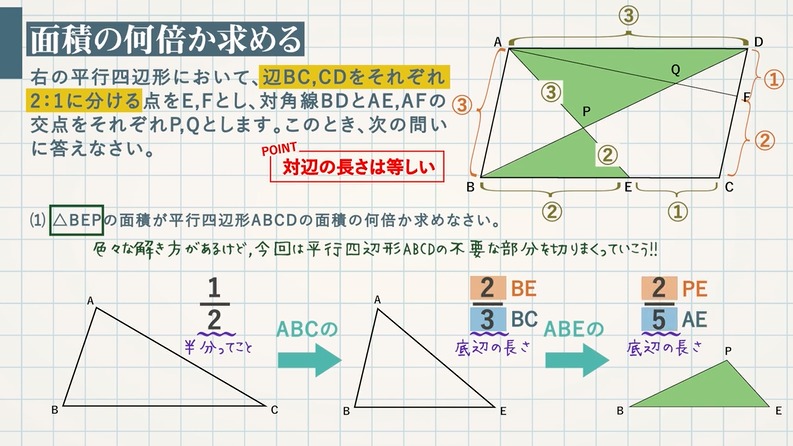



相似分野の応用問題 ラスボスっぽいの 多分それ連比です 面積の比 何倍 を求める問題も含めてかんたんな方法を解説します 教遊者
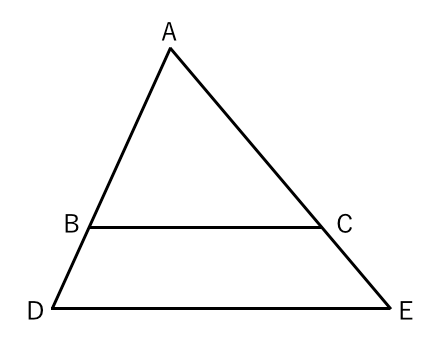



相似な図形 面積の比 苦手な数学を簡単に



Homeroom 数学の入試問題を解くとき大切なこと 正しい入り口から入らないと問題は解けない 平面図形 相似 働きアリ




中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 リョースケ大学
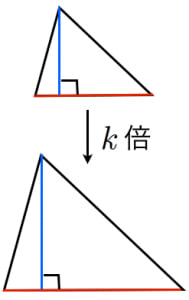



相似比と面積比 体積比の公式の証明 高校数学の美しい物語



1




数学 最重要 高さ共通 と 相似 面積比 集中特訓 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




平面図形をマスター 三角形の面積比 応用編その2




図形の面積比 知っている人は5秒以内には解ける面積比の裏技 Youtube
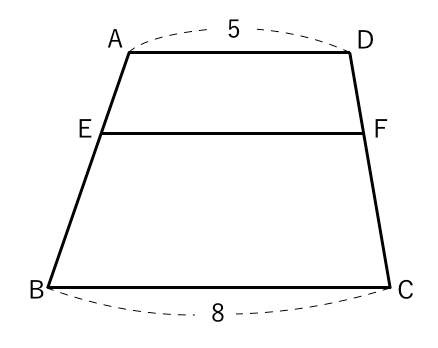



相似な図形 計算 台形 練習問題 苦手な数学を簡単に
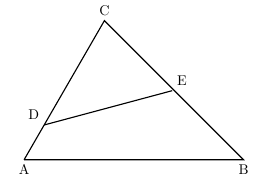



線分比と面積比の問題の解法 夢を叶える塾




平面図形をマスター 三角形の面積比 応用編その2




中学数学 相似な図形の面積比 中学数学の無料オンライン学習サイトchu Su



相似比とは 1分でわかる意味 面積比 四角形と三角形の問題
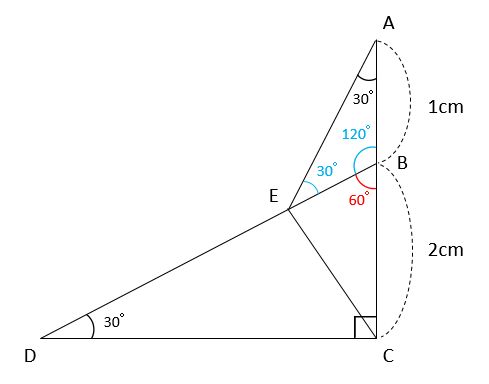



相似比と底辺比から面積比を求める 基準となる三角形を探せ みみずく戦略室




面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学




3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく
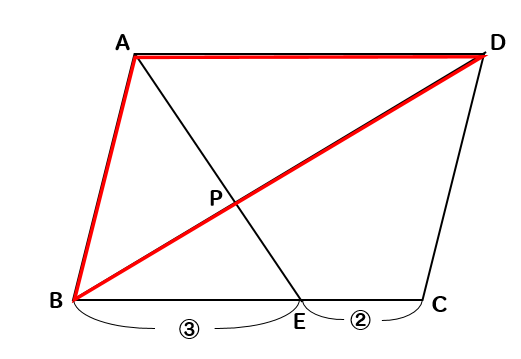



相似 平行四辺形と面積比の問題を徹底解説 数スタ




数学問題 知っている人は5秒で解ける三角形の面積比 暇つぶしに動画で脳トレ



相似問題より 台形の面積比公式 中学入試算数68分野別解法
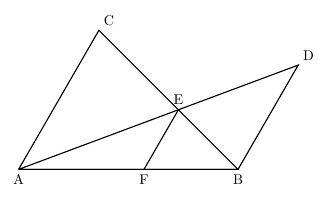



線分比と面積比の問題の解法 夢を叶える塾




相似比と面積比 無料で使える中学学習プリント




辺の比と面積比問題 考え方1 Youtube



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生




中3数学基礎 本当に使える裏技 相似の問題で差をつけろ 定期テストや高校入試に レオンの中学数学探検所




面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学



図形が不得意な子は 高度な図形問題 を解くときこの3点を気をつけよう 算数数学が苦手な子専門のプロ家庭教師みかん先生
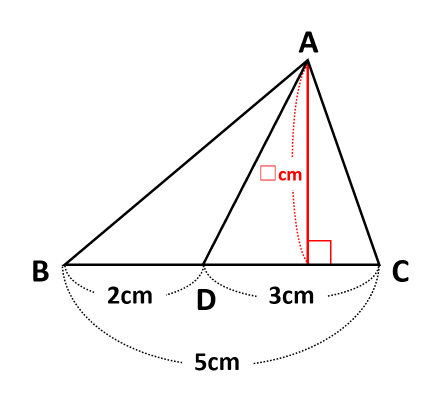



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ
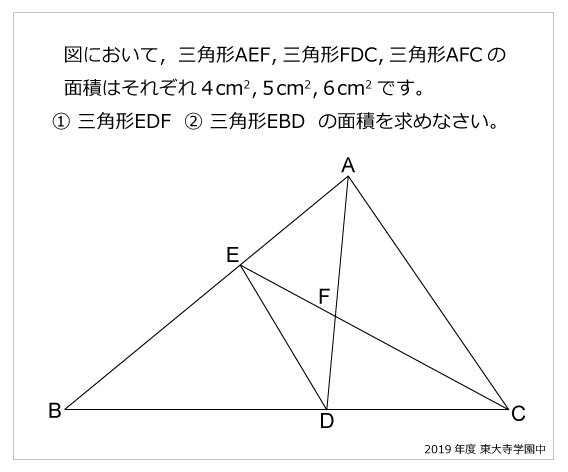



今年の1問 19年東大寺学園中 応用ベンツ 算数星人のweb問題集 中学受験算数の問題に挑戦




平面図形をマスター 三角形の面積比 応用編その2



相似とは 三角形の相似条件 記号 相似比 面積比 証明問題 受験辞典



中3数学相似な三角形の面積比の応用の問題がわかりません 解き方を読ん Yahoo 知恵袋



相似分野の応用問題 ラスボスっぽいの 多分それ連比です 面積の比 何倍 を求める問題も含めてかんたんな方法を解説します 教遊者



高校入試対策数学 面積比に関する対策問題 Pikuu



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ



1




相似な図形 面積比の問題 苦手な数学を簡単に




三角形の相似から四角形の面積比へ 開成中学2018入試 算数 問題1 7 テンメイのrun bike




小学6年生 算数 10月 辺の比と面積の比 速さ 1 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ



図形問題が驚くほど得意になる基本問題とは あおぞら塾
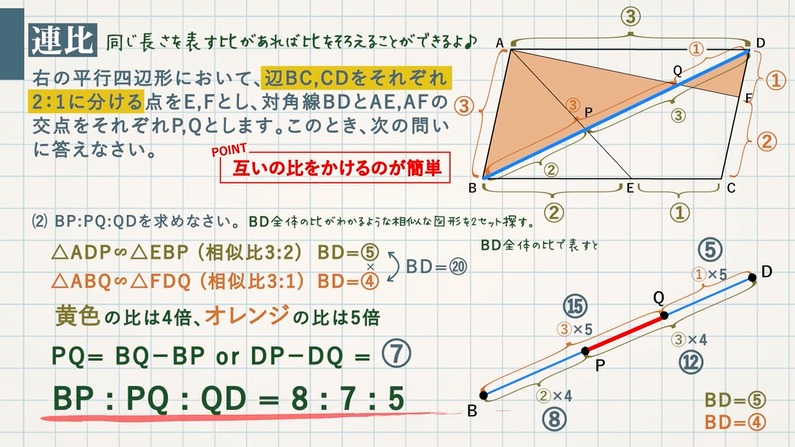



相似分野の応用問題 ラスボスっぽいの 多分それ連比です 面積の比 何倍 を求める問題も含めてかんたんな方法を解説します 教遊者
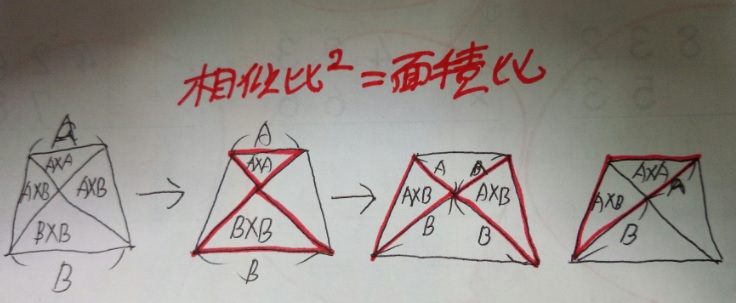



面積比と相似 図形の面積比は相似比の2乗 中学
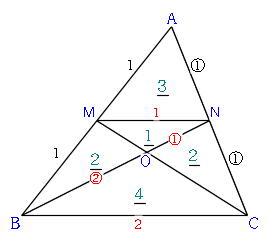



Mathematics 相似 4 面積と比 面積比は となりあった三角形で求める 働きアリ




中3数学 図形と相似27 相似な図形の面積比 すべて無料 星組の中学数学講座



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生




平面図形をマスター 三角形の面積比 応用編その2




かみのドリル 相似




補助線の引き方 日々の学習 兄中学受験



数学i Aチェック リピート 第4章 2図形への応用 8 相似形の面積比 Pukiwiki
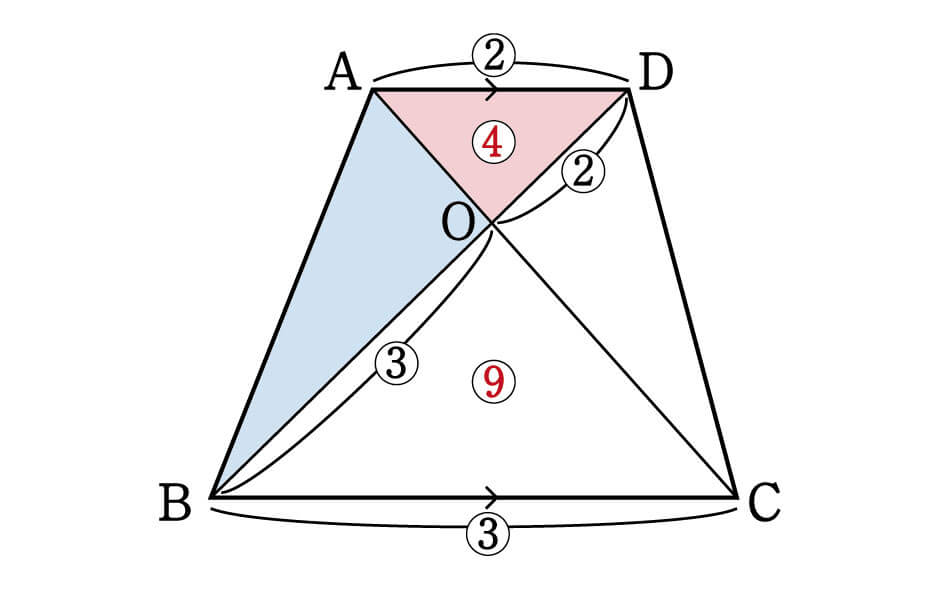



数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




数学 中3 53 相似と面積 応用編 Youtube



0 件のコメント:
コメントを投稿